Note 3 - Demonstration that Diagonal Lines are of Zero Magnitude

It can be shown quite easily that the diagonal lines = 0.
 

Below is drawn a circle of unit radius in the complex plane where the horizontal (x-axis) is real and the vertical (y-axis) is imaginary.

 

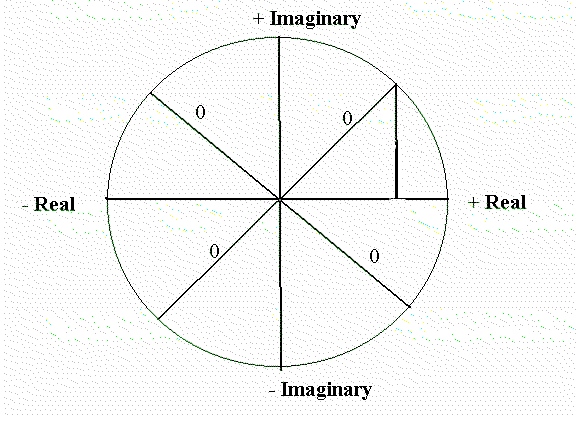
The horizontal (x axis) gives the real roots + 1 and - 1.

The vertical axis (y axis) gives the imaginary roots + i and  -i (where i = square root of -1)
 

Using the Pythagorean Theorem the magnitude of the diagonal axes - in each of the quadrants = 0.

(The triangle in the UR quadrant illustrates this point. Because the diagonal lines are drawn an equal distance from both x and y axes, the magnitude of the horizontal and vertical lines of triangle are similar in real and imaginary terms i.e. 1/(square root of 2) and 1/(square root of 2 i) respectively.

Therefore the square on the diagonal line of the triangle (i.e. hypotenuse) is equal to the sum of the squares of the other two sides.

So the diagonal line = 1/(square root of 2)² + 1/(square root of 2 i)² = 1/2 - 1/2 = 0.
 

Alternatively we can represent this diagonal line as the sum of coordinates of both x and y axes (the horizontal and vertical lines) i.e. 1/(square root of 2) + 1/(square root of 2 i)

= 1/(square root of 2) * (1 + i)

Now if for convenience we let k = 1/(square root of 2) then the diagonal line in the Upper Right Quadrant can be represented as k(1 + i).

In similar fashion the diagonal line in the Upper Left Quadrant can be represented as
k(- 1 + i).

The diagonal line in the Bottom Right Quadrant is k(1 - i).

Finally the diagonal line in the Bottom Left Quadrant is k(- 1 - i).
 

As we have shown, these diagonal lines (in each quadrant) can alternatively be viewed as null lines = 0.
 

Just as there are two equally valid ways for giving mathematical expression to the diagonal lines in analytic terms, equally it is also true in holistic terms, demonstarting the fundamental dynamic relationship as between form and emptiness (and emptiness and form).